Перевод статьи Дэвида Андерсона, размещённой на djaa.com.
Оригинал можно прочитать здесь.
Последней модой в сообществе гибкой разработки ПО является популяризация использования стоимости задержки для определения приоритетов. Многие читатели знают, что я был сторонником определения приоритетов в зависимости от «Стоимости задержек», и в моей книге 2003 года «Agile Management for Software Engineering» («Гибкое управление в разработке программ») были несколько алгоритмов, связанных со стоимостью задержки. Тем не менее, я вижу в мире много дезинформирующих, упрощенных и потенциально опасных руководств по использованию стоимости задержки, и пришло время внести некоторую ясность.
Большая часть материалов по стоимости задержки в Agile-пространстве основана на ссылках и модификациях уравнения WSJF (Weighted Shortest Job First — взвешенная продолжительность самой короткой задачи) из последней книги Дональда Г. Рейнертсена The Principles of Product Development Flow: Second Generation Lean Product Development («Принципы потока разработки продукта: второе поколение бережливой разработки продукта»).
Суть уравнения WSJF — это общая прибыль за весь срок службы, разделённая на продолжительность проекта разработки продукта.
В первых нескольких публикациях из этой серии я хочу рассмотреть, что мы знаем о знаменателе в этом уравнении — продолжительности проекта. WSJF также применяется в некоторых фреймворках для определения приоритетов пользовательских историй, функций и пр. Я не верю, что это хотя бы отдалённо уместно, и я хочу начать с объяснения того, что мы знаем о продолжительности таких пользовательских историй или функций, и пояснения, почему использование продолжительности в знаменателе уравнения WSJF не подходит для сравнительной оценки, выстраивания последовательности и приоритизации детализированных рабочих элементов, таких как пользовательские истории.
Что мы знаем о продолжительности: индивидуальные активности
24 февраля 2001 года я впервые опубликовал в своём блоге uidesign.net 5-балльную степенную шкалу для оценки размера и трудоёмкости функций в методе разработки, управляемом функциями.
Позднее, сравнивая мои данные с некоторыми известными сторонниками экстремального программирования (XP), такими как Тим Маккиннон, я понял, что лондонская школа написания пользовательских историй создаёт пользовательские истории схожего размера и сложности. Эта шкала формально появилась в моей книге 2003 года Agile Management for Software Engineering («Гибкое управление разработкой программного обеспечения»). Впервые я использовал её в проекте в Дублине (Ирландия) летом 1999 года.
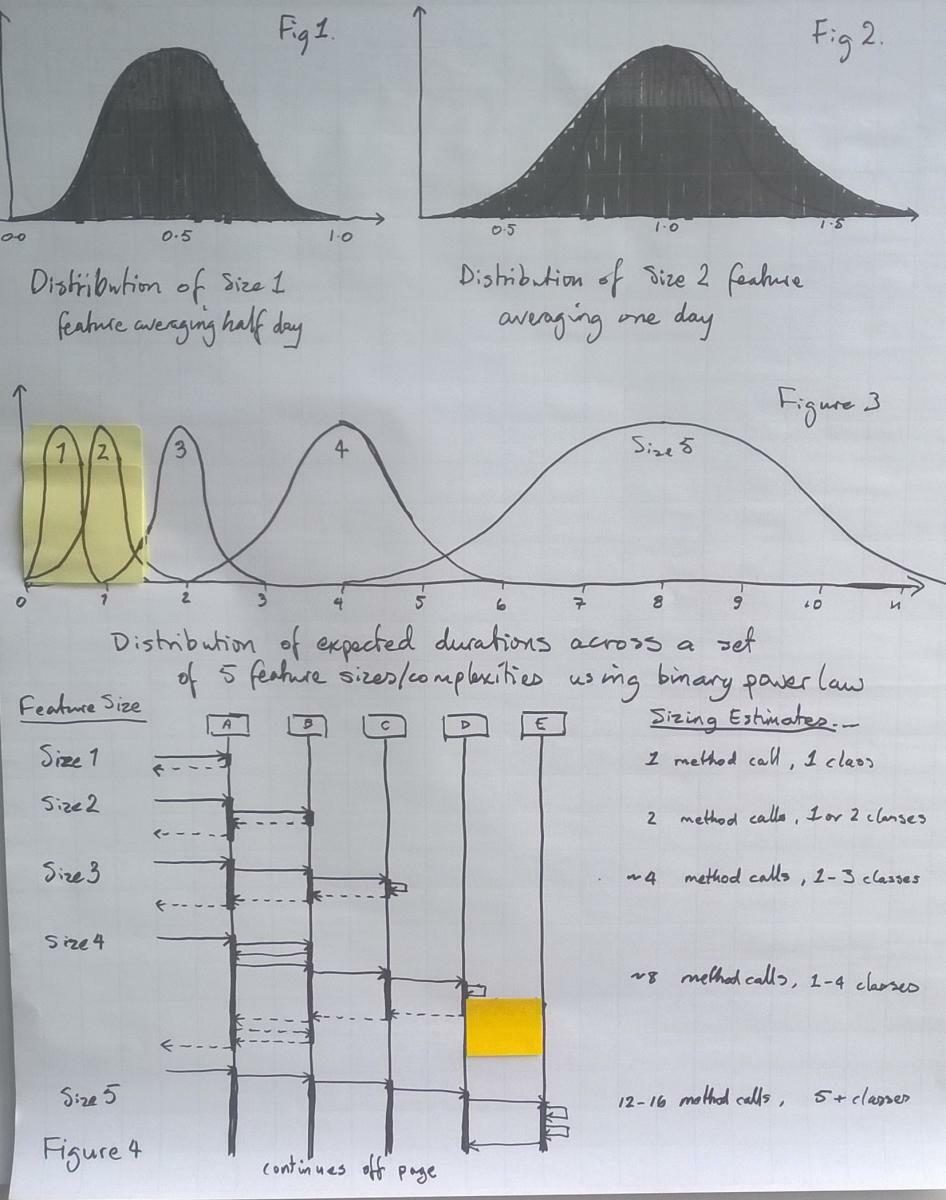
На Рис. 1 показана шкала. Это не случайные данные. Она не основана на «оценке» или разговорах. Она основана на анализе. Другими словами, она полностью детерминирована. Управляемая структура предложения для написания функций в методе разработки, управляемом функциями, позволяет специалисту в данной области быстро оценить, как эта функция повлияет на код. Предложение содержит подсказки для имени метода, класса, в котором будет закодирован метод, и возвращаемого значения из метода. Зная возвращаемое значение, кто-то, владеющий этой техникой, может почти с первого взгляда оценить, по скольким классам потребуется перемещаться для получения желаемого результата. У проектирующего дизайн оценщика появляются другие источники информации кроме собственного суждения. Он точнее оценивает, что дизайн может повлечь за собой с точки зрения классов, к которым осуществляется доступ, и вызовов методов.
Итак, я создал 5-балльную шкалу: функционала размером от 1 до 5. Я оценил, что средний уровень трудоёмкости для такого функционала возрастёт по квадратичному закону: 0,5 дня; 1 день; 2 дня; 4 дня; 8 дней и более.
Предположим, что мы выбрали правильный размер. Это разумное предположение, поскольку более 90% функций, измеренных с использованием этого метода, вероятно, будут иметь правильный размер., Но всё ещё маловероятно, что задача, такая как проектирование и написание кода для функционала— фактически написание всех вызовов методов и всех модульных тестов — займёт именно среднее время. Фактически, время, вероятно, будет случайным и достаточно равномерно распределённым.
Если бы у нас было достаточно точек данных (несколько сотен) и не было многозадачности, задержек или блокировки по другим зависимостям и сбоям во время выполнения задачи, мы могли бы ожидать обычного нормального распределения с масштабом примерно на 50% выше и ниже среднего. Таким образом, функционал размера 2, выполнение которых занимает, в среднем, 1 день, должны выполняться за 0,5−1,5 дня.
Существует вырожденный случай, когда многозадачность не искажает форму нормального распределения. Здесь скорость переключения задач в два или несколько раз выше, чем минимально возможная продолжительность задачи: если у нас задача длиной 31 минуту, и мы переключаем задачи каждые 15 минут, есть одинаково случайный шанс, что все задачи будут прерваны и следовательно, распределение останется нормальным. Конечно, такое быстрое переключение задач означало бы, что процесс чрезвычайно неэффективен, и, как следствие, всё распределение было бы сдвинуто вправо и масштабировано вправо. Вот почему это случай генерирования: он существует в математической теории, но больше он нигде не существует.
Если теперь учесть, что самая короткая задача может занять 30 минут (0,5 часа), а самая длинная — 12 дней (96 часов), мы получим разброс вариаций для трудоёмкости по функциям, который охватывает 200 наименьших продолжительностей. Множитель 200 соответствует результатам Рейнертсена. Вероятно, разумно предположить, что время выполнения задачи будет охватывать как минимум 50-кратный минимальный размер независимо от используемого процесса. Опять же, эти данные представляют собой «уровень трудоемкости» и по-прежнему предполагают отсутствие переключения между задачами, задержек и нарушений обслуживания.
Теперь, давайте рассмотрим разброс вариативности размеров функций в данном проекте…
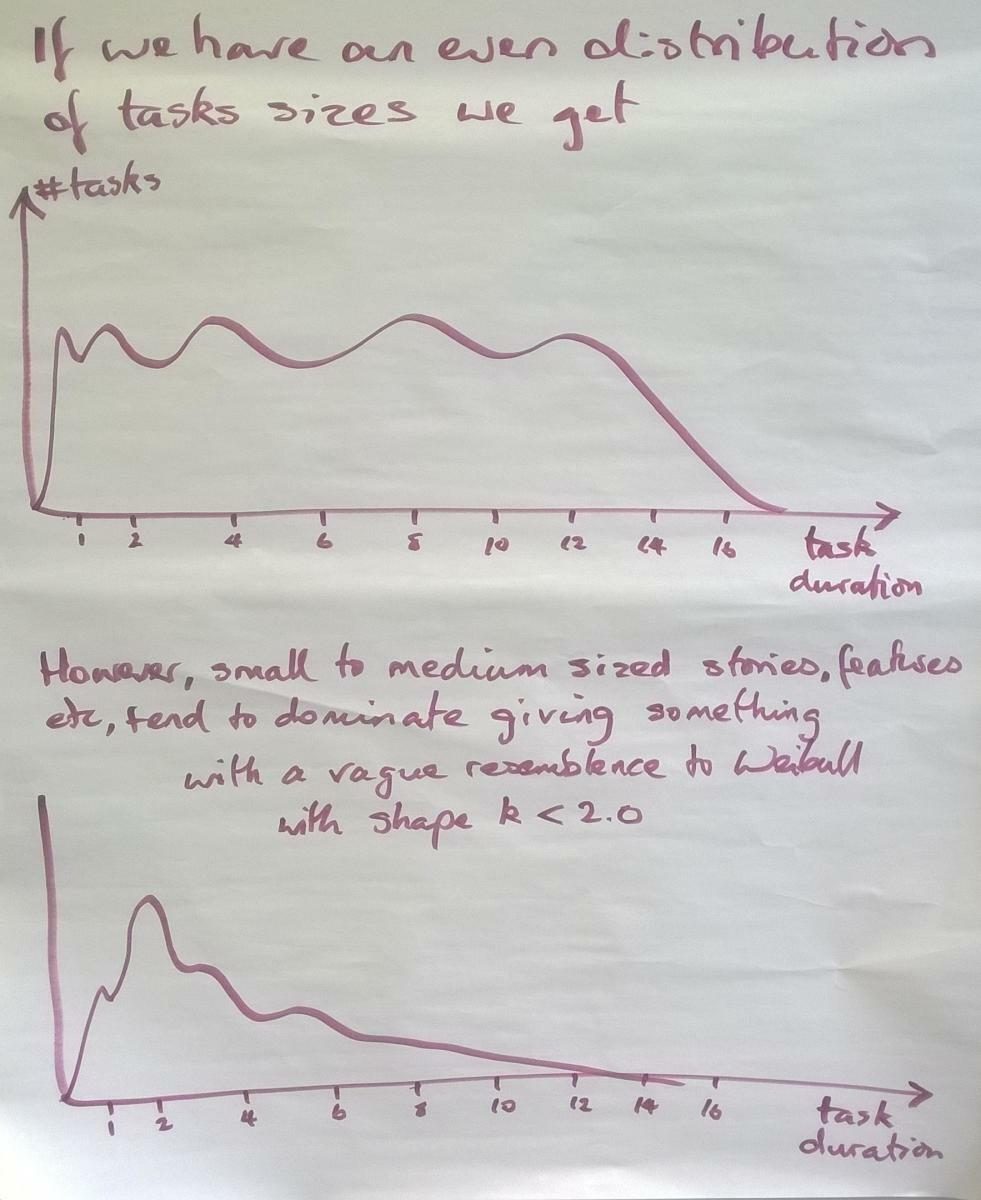
На Рис. 2 показано, как может варьироваться распределение продолжительности задач, когда мы суммируем распределения для каждого размера функционала. Другими словами, если мы будем рассматривать весь функционал просто как функции, сколько времени может потребоваться для завершения их разработки? На верхней диаграмме показано мультимодальное распределение для равномерного распределения функций, то есть у нас примерно такое же количество размеров 1, как и размеров 2, 3, 4 и 5. Такого равномерного распространения я ещё никогда не видел. Более типичным является перекос в сторону малого и среднего размера, когда наиболее распространённым является размер 2. Это даёт распределение, более похожее на нижний пример.
Как многозадачность, задержки и нарушения влияют на форму распределения?
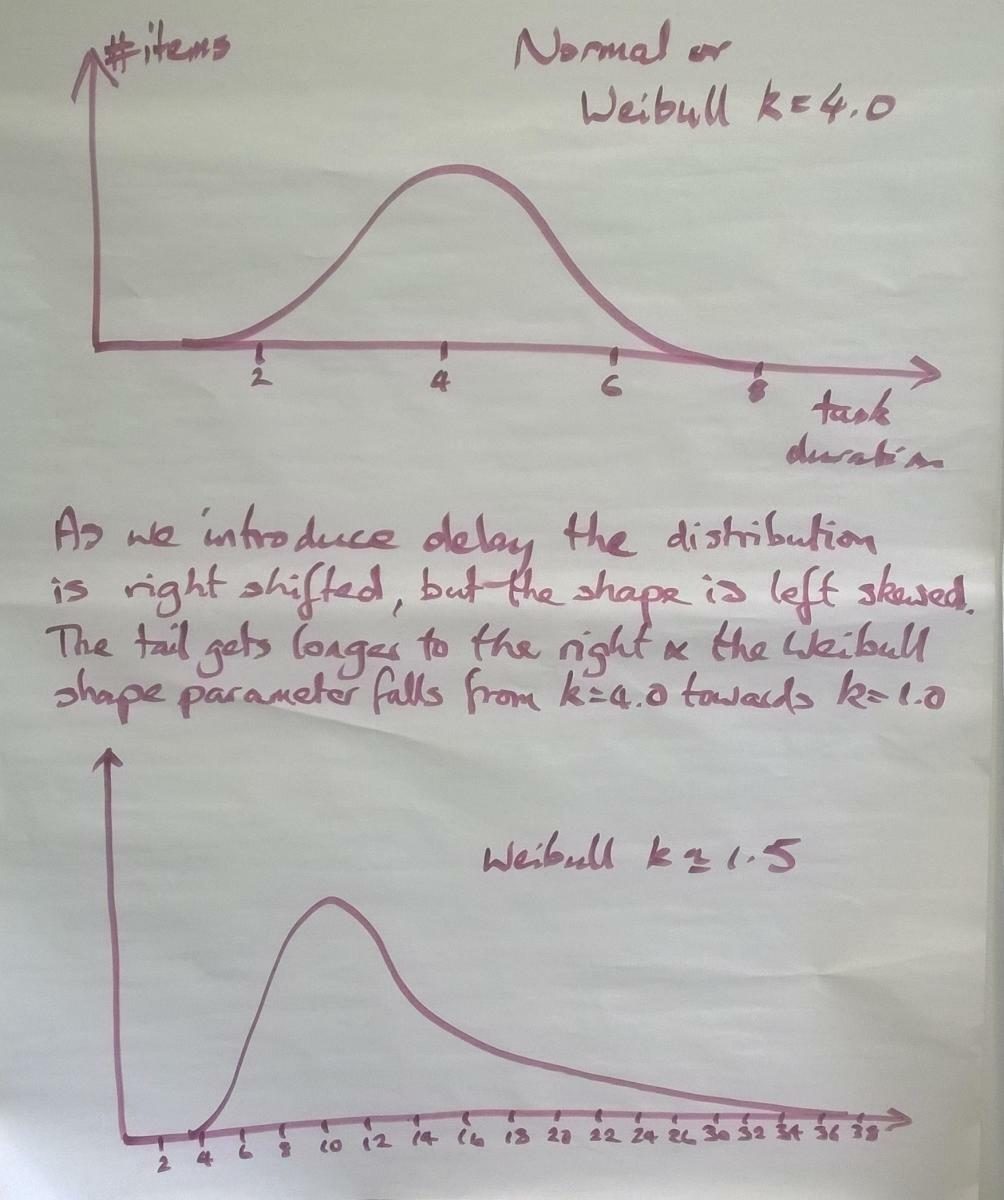
Если уменьшается вероятность задержки чего-либо, хвост распределения постепенно смещается вправо. Следовательно, у долгосрочных задач больше шансов быть отложенными, а у отложенных — больше шансов быть отложенными еще раз. Вот что даёт длинный хвост справа.
Математически, когда мы тянем хвост вправо, параметр формы в уравнении Вейбулла сокращается. Мы называем это изменением формы или искажением распределения слева. Все распределение физически сдвинуто вправо. Обратите внимание, что я разместил шкалу на оси X. Мода|медиана|среднее арифметическое в нормальном распределении составляют 4,0, в то время как у нижней кривой мода равна 11, медиана примерно равна 11 и среднее арифметическое примерно равно 12. Таким образом, средняя продолжительность задачи увеличилась в 3 раза из-за задержек и многозадачности.
Средние значения легко объяснить, но именно хвост распределения представляет основную часть риска. В идеальной ситуации с нормальным распределением задача выполняется максимум за 8, в то время как после введения многозадачности, задержек и нарушений обслуживания максимум вырос до 38.
На Рис. 3 показан перекос в распределении для функционала размера 4, когда возникает некоторая многозадачность, а также задержка из-за зависимостей и нарушения обслуживания (т. е. недоступности работника, например, из-за болезни или службы в суде присяжных). Вы можете себе представить, когда мы моделируем это для всех пяти размеров, а затем свёртываем в единое распределение, подобное показанному на Рис. 2, мы получаем ещё более выраженный эффект длинного хвоста.
Все это показано для одного действия. Мы даже не начали рассматривать рабочий процесс, состоящий из нескольких действий с задержками между ними. Я расскажу об этом во второй статье из этой серии.
Итак, что мы знаем о продолжительности задач?
Таким образом, если у вас есть только детерминистский метод анализа, позволяющий быстро и дешёво оценить размер и сложность, вы сможете разбить продолжительности задач по таксономии категорий.
Как указал Юрген Аппело в своей книге Management 3.0 («Менеджмент 3.0»), ряд Фибоначчи, столь любимый агилистами, на самом деле не встречается в природе. Кроме того, его индекс недостаточно редок: история, оценённая как 3 по шкале Фибоначчи, скорее всего, будет иметь вес 1, 2, 4 или 5, в то время как альтернативы выше и ниже по шкале Фибоначчи — 2 и 5. Следовательно, он совершенно случаен, для пользовательских историй с весом 2, 3 или 5. Вероятность того, что вес на самом деле 3, составляет менее 50%. Если мы предположим, что во время выполнения задачи никогда не происходит упреждения, корреляция между её размером или сложностью и её реальной продолжительностью всё равно очень мала. Конечно, упреждение действительно происходит, и, следовательно, на самом деле нет никакой корреляции между количеством баллов за историю и её продолжительностью. Это делает продолжительность проекта бесполезной в качестве средства сравнительной оценки и определения приоритетов в уравнении, таком как WSJF, поскольку существует высокая вероятность того, что знаменатель в уравнении для каждой задачи или элемента неверен. Это может сильно повлиять на результат или рейтинг, основанный на результатах уравнения. Как следствие этого, размер информации практически не имеет никакой ценности, и для целей расчёта продолжительности мы можем также предположить, что все пользовательские истории имеют одинаковый размер. Мы не можем детерминировано оценить продолжительность любого элемента данного типа по сравнению с продолжительностью другого элемента того же типа. Этот анализ исключает размер пользовательской истории как полезный параметр в уравнении WSJF.
С другой стороны, степенные законы и распределения Вейбулла, включая (k = 4,0) нормальное распределение и (k = 1,0) экспоненциальное распределение, действительно существуют в природе. Поэтому гораздо более вероятно, что размер для пользовательских историй следует степенному закону. В 2009 году Юрген обнаружил, что я опубликовал такой степенной закон, и самое раннее упоминание о нём в Интернете датируется 24 февраля 2001 года. Даже со степенной шкалой существует некоторая, но меньшая вероятность того, что фактическая продолжительность наложится на элемент другого размера или сложности. Надеюсь, Рис. 1 убедит вас, что балльная шкала, оценивающая размер и сложность, не имеет смысла при оценке продолжительности задачи для целей сравнительной оценки и определения приоритетов. Если нет, то, возможно, вторая статья из этой серии приведёт вас к выводу, что оценка продолжительности с целью использования её в качестве знаменателя в уравнении WSJF бесполезна при детализации задач, историй, функций или эпиков.
Из других результатов мы знаем, что продолжительность задач обычно имеет разброс до 200 раз. Разработанная мною степенная шкала метода разработки, управляемая функциями, демонстрирует это довольно легко, если предположить, что рабочий день составляет 8 часов. В своей книге 2003 года я предполагал, что в день возможно только 5,5 часов продуктивной работы. Использование меньшего числа по-прежнему даёт кратность 132 от наименьшей к наибольшей функции.
Итак, мы понимаем, что проблема оценки продолжительности задач, таких как разработка пользовательской истории, является нелинейной, но мы также понимаем, что она не является детерминированной. Если мы знаем, например, из детерминистского анализа, что эта функция включает 3 класса и 5 вызовов методов, мы все равно не можем сказать с детерминированной точностью, сколько времени займет её реализация. Продолжительность — это случайная величина, распределённая по закону Вейбулла.
Итак, в целом, для индивидуального действия в рабочем процессе продолжительность задачи до завершения действия изменяется нелинейно и не является детерминированной. Она распределена приблизительно по закону Вейбулла с параметром формы в диапазоне 1,0 < k < 4,0 и, наиболее вероятно, в диапазоне 1,3 < k < 2,0. Разброс от самого короткого до самого длинного значений может составлять до 200 кратчайших значений.
Если вы пытаетесь «оценить» продолжительность такой задачи, как проектирование, кодирование, тестирование пользовательской истории, вы, в основном, пытаетесь угадать. Вы бросаете кости и наносите удары в темноте. Фактическое истекшее календарное время (или продолжительность) действия, вероятно, будет сильно отличаться от вашей «оценки».









