Что мы знаем о продолжительности: сравнение. Часть 3

Это третья часть моей серии статей, в которой развенчивается наше восхищение определением приоритетов с использованием стоимости задержки и соответствующих уравнений теории очередей, таких как WSJF (взвешенная продолжительность самой короткой задачи) или его производных, таких как CD3 (стоимость задержки, поделенная на продолжительность). Я искренне верю, что мы все должны быть защищены от этого культа. Я не думаю, что он хорошо служит инициативам бережливой разработки или Канбан — люди просто не могут получить надежные числа для этих уравнений приоритизации, и даже если бы они могли, лежащая в основе математика неадекватна. Мне понадобится 6 частей, чтобы полностью разобраться в бесполезности и бесперспективности этих методов. Это третья, последняя часть, где мы исследуем знаменатель в этих уравнениях, продолжительность…

Первые две статьи из этой серии должны были убедить вас в том, что если какие-либо два элемента относятся к одному типу, например, пользовательские истории, то для нас невозможно заранее оценить их соответствующие продолжительности.

Продолжительность обоих элементов одного типа будет соответствовать одной и той же функции распределения вероятностей, она будет полностью недетерминирована. Следовательно, для двух элементов одного типа мы должны априори рассматривать их соответствующие продолжительности как идентичные. Другими словами, продолжительность будет постоянной для всех приоритетов однотипных элементов, например пользовательских историй. Это верно, даже если пользовательские истории были «подобраны по размеру» с использованием некоторого механизма относительной оценки, например, баллов за историю. Нет корреляции между «размером» и продолжительностью.

Таким образом, любая форма, использующая для определения приоритетов элементов одного и того же типа уравнение, связанное со стоимостью задержки, фактически должна полностью игнорировать продолжительность в качестве входных данных — продолжительность должна рассматриваться как константа для всех элементов одного и того же типа. Это исключает использование WSJF или CD3 в качестве механизма приоритезации для многих классов проблем: определение приоритетов невыполненных пользовательских историй в проекте или выстраивание последовательности вытягивания для запросов на изменение в рабочем процессе по предоставлению услуг сопровождения программного обеспечения.

Итак, остается вопрос: существуют ли обстоятельства, при которых мы можем сравнивать продолжительность, и если да, как нам это делать?

Проекты имеют тенденцию быть достаточно разнородными, поэтому, хотя мы используем одно название типа — «проект» — на самом деле они уникальны каждый по отдельности: у них разное количество функций, выделенных людей и ресурсов. Допустим, что уровень неоднородности не соответствует действительности в серии выпусков продукта, где каждый выпуск имеет примерно одинаковый размер с точки зрения свойств или функций, разработанных за один и тот же период времени одной и той же командой специалистов. Тогда мы будем рассматривать каждый выпуск, как элемент одного и того же типа, и его продолжительность будет считаться постоянной, даже если эта константа является функцией распределения вероятностей.

Итак, если у нас есть разнородные проекты, как рассчитать продолжительность? Лучший метод, известный нашему сообществу, — моделирование Монте-Карло. Он становится одновременно популярным и легкодоступным. SwiftKanban имеет встроенное моделирование Монте-Карло в качестве стандартной функции. Существует также несколько других нишевых инструментов точечных решений от лидеров нашего сообщества, таких как Трой Магеннис и Ларри Макчероне. Если мы смоделируем где-то 1000 итераций проекта с использованием метода Монте-Карло, мы получим функцию распределения вероятностей для продолжительности проекта. На Рис. 1 показаны 6 различных сценариев функций распределения вероятностей для двух проектов, обозначенных (а) зеленым и (b) фиолетовым.

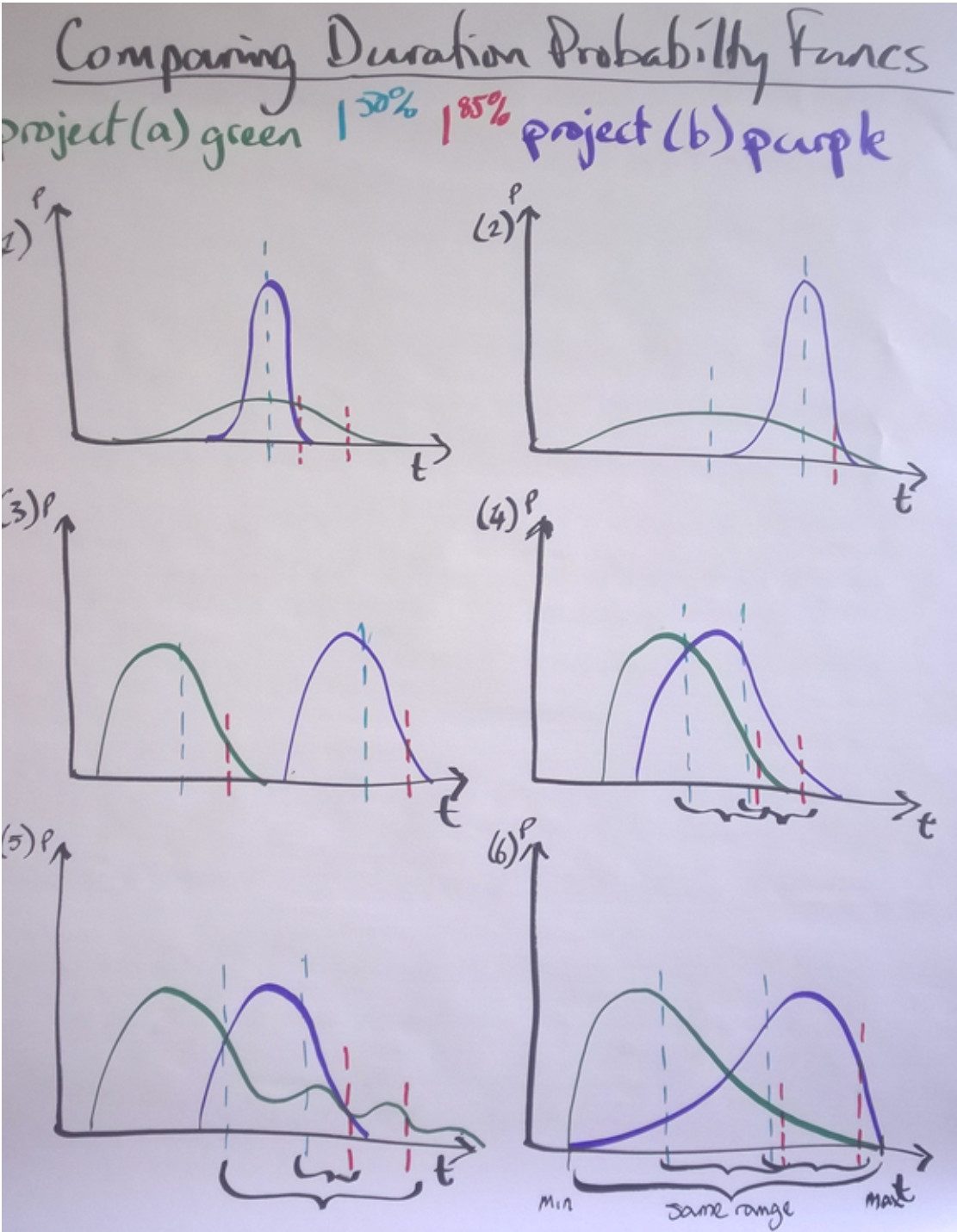
Итак, если мы рассмотрим эти два проекта, мы увидим, что теперь у нас есть разные профили для их распределения. Однако, если бы мы использовали уравнение WSJF (или CD3), чтобы определить приоритеты и выбрать один из предметов в качестве следующего для запуска в нашем портфеле, нам понадобится лишь одно значение для знаменателя — значение продолжительности. Мы не можем использовать функцию распределения вероятностей. Вопрос в том, какое значение выбрать?

Джошуа Арнольд, популяризатор CD3, рекомендует выбирать минимальное значение. Один из наших общих клиентов называет это «продолжительностью мечты», т. е. наилучшим возможным случаем, минимальной возможной продолжительностью. В нашей функции распределения вероятностей это будет значение процентили 1%, которое всегда будет визуально находиться в левой части графика функции.

Если мы рассмотрим сценарий 1, у проекта (a) самая короткая продолжительность, но на самом деле у проекта (b) есть около 40% шансов на окончательное завершение раньше проекта (a). Между тем, разница между самыми короткими значениями для (a) и (b) составляет 1 к 10 000, а вероятность того, что (b) завершится раньше (a), составляет примерно 6 из 10. Таким образом, продолжительность мечты — плохой выбор в этом сценарии, по крайней мере, 6 раз из 10.

Если мы перейдем к сценарию 2, теперь больше шансов, что (a) завершится раньше (b), вероятно, примерно в 75% случаев, но разница в минимальных значениях для (a) и (b), скорее всего, будет приводить к очень искаженным результатам уравнения. Если мы просто хотим выбирать между этими двумя проектами, это тривиально, но если бы было больше вариантов для ранжирования, тогда выбор минимального значения был бы очень проблематичным.

В сценарии 3 использование минимальной продолжительности, вероятно, приемлемо, но мы по-прежнему предполагаем «лучший исход», и это, как правило, неразумный подход к управлению рисками.

В сценарии 4 минимальная продолжительность, вероятно, является справедливым методом сравнения, но мы также должны признать вероятность приблизительно 30% того, что (b) завершится раньше (a), и, следовательно, минимальное значение безопасно только в 70% случаев, и мы не можем определить это априори.

В сценарии 5 проект (a) создает функцию распределения вероятностей мультимодальной продолжительности. Это говорит о том, что проект подвержен внешним рискам, вызывающим задержку. Если предположить, что мы не можем заранее определить, возникнут ли эти риски на самом деле, тогда использование минимального значения для продолжительности (а) и (b) реально опасно. Если мы можем определить, существует ли на самом деле один или несколько рисков, тогда мы хотели бы использовать минимальное число для продолжительности с учетом известного риска, то есть мы хотели бы смоделировать продолжительность проекта с исключенной из нашего набора данных возможностью того, что риск не произойдет. Тогда у нас останутся две одномодальных функции распределения вероятностей для (a) и (b), которые могут напоминать один из первых 4 сценариев.

В сценарии 6 минимальные (и максимальные) значения идентичны, но проект (a) имеет гораздо более высокую вероятность завершения до (b) — примерно в 85% случаев. В этом случае выбор минимальной продолжительности для сравнения — бесполезный нонсенс.

Учитывая, что смоделированные продолжительности проекта, как правило, являются функциями с тонким хвостом, разница между медианой (процентилью 50%) и средним арифметическим (для набора данных возможных результатов) несущественна. Мы можем выбрать использование медианы или среднего арифметического, главное — быть последовательными. В этом случае я набросал медианные значения на функции распределения вероятностей на Рис. 1.

• В сценарии 1 у обоих проектов одинаковое медианное значение, но при этом продолжительность проекта (a) непостоянна и сильно варьируется, в то время как продолжительность проекта (b) является устойчивой с низкой изменчивостью. В результате вероятность завершения (b) до (a) гораздо выше. Использование среднего значения, одинакового для обоих проектов, приведет к ненадежным результатам.
• В сценарии 2 среднее значение дает более справедливое сравнение и определенно является лучшим выбором, чем минимальное значение.
• В сценарии 3 среднее значение дает справедливое сравнение, и если нам нужно что-то использовать, это очень разумный выбор.
• В сценарии 4, опять же, среднее значение дает справедливое сравнение, но оно маскирует возможность того, что (b) завершится раньше, чем (a), возможно, в 30% случаев.
• В сценарии 5 медиана вводит в заблуждение, поскольку (a) выглядит лучше, чем (b). На самом деле значения среднего арифметического будут ближе друг к другу и покажут вариант (b) в более благоприятном свете. Независимо от этого, учитывая риски, связанные с длинным мультимодальным хвостом в проекте (a), (b), не имеет достаточных шансов при использовании для сравнения медианы или среднего арифметического.
• В сценарии 6 медиана фактически дает достаточно разумную сравнительную оценку рисков, связанных с завершением проектов.

Таким образом, в целом медиана или среднее арифметическое оказывается лучше минимума для этих шести сценариев.

Красными пунктирными линиями на Рис. 1 показаны процентили 85% функций распределения вероятностей продолжительности проекта. Теперь мы имеем дело с наихудшим случаем: вероятность того, что проекты продлятся так долго, составляет 1 из 7, и, следовательно, 1 из 49 (или около 2%), что они оба будут длиться как минимум столько времени. Это гораздо более консервативный метод сравнения, чем лучший случай, который мы рассмотрели вначале.

Теперь в сценарии 1 (b) выглядит более привлекательно, чем (a), что является справедливой оценкой.

В сценарии 2 (a) и (b) выглядят одинаково, но на самом деле (a) должен быть гораздо более привлекательным, так как он имеет шанс примерно 60% всегда завершиться до (b).

В сценарии 3 процентиль 85% дает нам справедливое сравнение и (а) выглядит более привлекательно. Это лучший выбор, чем медиана или среднее арифметическое? Трудно сказать, но процентная разница между двумя значениями процентили 85% будет ниже, чем при использовании для сравнения медианы или среднего арифметического, и, следовательно, вариант (b) выглядит относительно более привлекательным при использовании процентили 85% по сравнению с процентилью 50% или средним арифметическим.

В сценарии 4 вариант (а) выглядит привлекательнее, чем (b), и это справедливое сравнение.

В сценарии 5 (b) теперь выглядит более привлекательно, чем (a), и это также может быть справедливым сравнением.

В сценарии 6 (a) выглядит более привлекательно, чем (b), и снова, вероятно, это справедливое сравнение, и соотношение между ними, вероятно, дает справедливую оценку различных рисков продолжительности.

Мы могли бы исследовать максимально возможное значение продолжительности, процентиль 99% функции распределения вероятностей, и это дало бы нам аналогичные, но противоположные результаты по сравнению с нашим лучшим вариантом сравнения.

Этого небольшого упражнения должно быть достаточно, чтобы продемонстрировать вам, что в зависимости от сравниваемых проектов и их соответствующих функций распределения вероятности продолжительности используется метод, используемый для сравнения их продолжительности как одного числа — лучший случай, худший случай, медиана, среднее арифметическое или процентиль 85% дадут разные результаты, некоторые из которых являются справедливой оценкой сравнительных рисков, а другие — нет. Ни одно решение не работает лучше всего в каждом сценарии.

Из этого я пришел к выводу, что для сравнения продолжительности проектов вам нужна вся функция распределения вероятностей, и вам нужно провести параллельное визуальное сравнение, а затем взвесить другие факторы, такие как предоставляемая ценность и сроки. Упрощение продолжительности до одного числа, независимо от того, каким образом это число получено, — нонсенс. Нам нужно отмести это предположение и начать надлежащим образом управлять риском продолжительности. В части 6 этой серии статей будет рассмотрен жизнеспособный метод для принятия правильных решений с оценкой риска для планирования, выстраивания последовательности и выбора проектов и других видов работ.